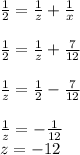Question

PLZ HELP ME ☻
`\[(xy)/(x + y) = 1, \quad (xz)/(x + z) = 2, \quad (yz)/(y + z) = 3\]` Solve system of equations

Answer 1

`x=(12)/(7) \\y=(12)/(5) \\z=-12`

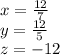
Explanation:

Let's re-write the equations in order to get the variables as separated in independent terms as possible \:

First equation:

`(xy)/(x+y) =1\\xy=x+y\\1=(x+y)/(xy) \\1=(1)/(y) +(1)/(x)`

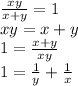
Second equation:

`(xz)/(x+z) =2\\xz=2\,(x+z)\\(1)/(2) =(x+z)/(xz) \\(1)/(2) =(1)/(z) +(1)/(x)`

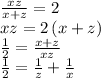
Third equation:

`(yz)/(y+z) =3\\yz=3\,(y+z)\\(1)/(3) =(y+z)/(yz) \\(1)/(3)=(1)/(z) +(1)/(y)`

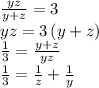
Now let's subtract term by term the reduced equation 3 from the reduced equation 1 in order to eliminate the term that contains "y":

`1=(1)/(y) +(1)/(x) \\-\\(1)/(3) =(1)/(z) +(1)/(y)\\(2)/(3) =(1)/(x) -(1)/(z)`

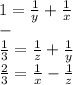
Combine this last expression term by term with the reduced equation 2, and solve for "x" :

`(2)/(3) =(1)/(x) -(1)/(z) \\+\\(1)/(2) =(1)/(z) +(1)/(x) \\ \\(7)/(6) =(2)/(x)\\ \\x=(12)/(7)`

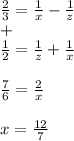
Now we use this value for "x" back in equation 1 to solve for "y":

`1=(1)/(y) +(1)/(x) \\1=(1)/(y) +(7)/(12)\\1-(7)/(12)=(1)/(y) \\ \\(1)/(y) =(5)/(12) \\y=(12)/(5)`

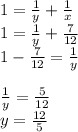
And finally we solve for the third unknown "z":

`(1)/(2) =(1)/(z) +(1)/(x) \\\\(1)/(2) =(1)/(z) +(7)/(12) \\\\(1)/(z) =(1)/(2)-(7)/(12) \\\\(1)/(z) =-(1)/(12)\\z=-12`