Question

Rebecca is a real estate agent who would like to find evidence supporting the claim that the population mean market value of houses in the neighborhood where she works is greater than $250,000. To test the claim, she randomly selects 35 houses in the neighborhood and finds that the sample mean market value is $259,860 with a sample standard deviation of $24.922. The test statistic t for a hypothesis test of H0 : μ = 250.000 versus Ha : μ > 250.000 is t 2.34 , which has 34 degrees of freedom. If 0.01 A) Fail to reject the null hypothesis that the true population mean market value of houses in the neighborhood where Rebecca works is equal to $250,000.

B) Reject the null hypothesis that the true population mean market value of houses in the neighborhood where Rebecca works is equal to $250,000.
C) There is enough evidence at the α-: 0.05 level of significance to support the claim that the true population mean market value of houses in the neighborhood where Rebecca works is greater than $250,000.
D) There is not enough evidence at the α-_ 0.05 level of significance to suggest that the true population mean market value of houses in the neighborhood where Rebecca works is not equal to $250,000.

Answer 1

There is enough evidence at the α-: 0.05 level of significance to support the claim that the true population mean market value of houses in the neighborhood where Rebecca works is greater than $250,000.

Explanation:

We are given that Rebecca randomly selects 35 houses in the neighborhood and finds that the sample mean market value is $259,860 with a sample standard deviation of $24.922.

Let
`\mu` = population mean market value of houses in the neighborhood.

So, Null Hypothesis,
`H_0` :
`\mu` = $250,000 {means that the population mean market value of houses in the neighborhood where she works is equal to $250,000}

Alternate Hypothesis,
`H_A` :
`\mu` > $250,000 {means that the population mean market value of houses in the neighborhood where she works is greater than $250,000}

The test statistics that would be used here One-sample t-test statistics because we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean market value = $259,860

s = sample standard deviation = $24,922

n = sample of houses = 35

So, the test statistics =
`(259,860-250,000)/((24,922)/(√(35) ) )` ~
`t_3_4`

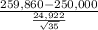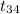
= 2.34

The value of t-test statistic is 2.34.

Also, P-value of the test statistics is given by;

P-value = P(
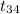`t_3_4` > 2.34) = 0.0137

Since our P-value is less than the level of significance as 0.0137 < 0.05, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the population mean market value of houses in the neighborhood where she works is greater than $250,000.