Answer:
Slopes of parallel lines are equal
Explanation:
On a coordinate plane, quadrilateral ABCD is shown. Point A is at (-2, -2), point B is at (-3, 4), point C is at (2, 2), and point D is at (3, -4).
The slope of the line segment BC is:
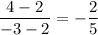
The slope of the line segment AD is:
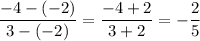
The slope of the line segment CD is:
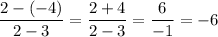
The slope of the line segment BA is:
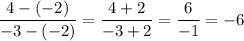
Because the slopes of parallel lines are equal. Therefore, ABCD is a parallelogram because both pairs of opposite sides are parallel.