Question

One end of an insulated metal rod is maintained at 100c and the other end is maintained at 0.00 c by an ice–water mixture. The rod has a length of 75.0cm and a cross-sectional area of 1.25cm . The heat conducted by the rod melts a mass of 6.15g of ice in a time of 10.0 min .find the thermal conductivity k of the metal?k=............ W/(m.K)

Answer 1

The thermal conductivity of the insulated metal rod is
`202.92\,(W)/(m\cdot K)`.

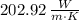Step-by-step explanation:

This is a situation of one-dimensional thermal conduction of a metal rod in a temperature gradient. The heat transfer rate through the metal rod is calculated by this expression:

`\dot Q = (k_(rod)\cdot A_(c, rod))/(L_(rod))\cdot \Delta T`

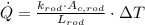
Where:

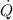`\dot Q` - Heat transfer due to conduction, measured in watts.

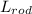`L_(rod)` - Length of the metal rod, measured in meters.

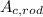`A_(c,rod)` - Cross section area of the metal rod, measured in meters.

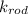`k_(rod)` - Thermal conductivity, measured in
`(W)/(m\cdot K)`.

Let assume that heat conducted to melt some ice was transfered at constant rate, so that definition of power can be translated as:

`\dot Q = (Q)/(\Delta t)`

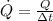
Where Q is the latent heat required to melt the ice, whose formula is:

`Q = m_(ice)\cdot L_(f)`

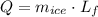
Where:

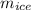`m_(ice)` - Mass of ice, measured in kilograms.

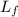`L_(f)` - Latent heat of fussion, measured in joules per gram.

The latent heat of fussion of water is equal to
`330000\,(J)/(g)`. Hence, the total heat received by the ice is:

`Q = (6.15\,g)\cdot \left(330\,(J)/(g) \right)`

`Q = 2029.5\,J`

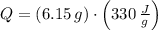
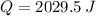
Now, the heat transfer rate is:

`\dot Q = (2029.5\,J)/((10\,min)\cdot \left(60\,(s)/(min) \right))`

`\dot Q = 3.382\,W`

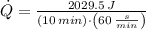
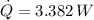
Turning to the thermal conduction equation, thermal conductivity is cleared and computed after replacing remaining variables: (
`L_(rod) = 0.75\,m`,
`A_(c,rod) = 1.25* 10^(-4)\,m^(2)`,
`\Delta T = 100\,K`,
`\dot Q = 3.382\,W`)

`\dot Q = (k_(rod)\cdot A_(c, rod))/(L_(rod))\cdot \Delta T`

`k_(rod) = (\dot Q \cdot L_(rod))/(A_(c,rod)\cdot \Delta T)`

`k_(rod) = ((3.382\,W)\cdot (0.75\,m))/((1.25* 10^(-4)\,m^(2))\cdot (100\,K))`

`k_(rod) = 202.92\,(W)/(m\cdot K)`

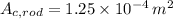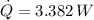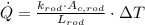
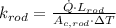
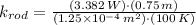
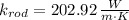
The thermal conductivity of the insulated metal rod is
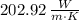`202.92\,(W)/(m\cdot K)`.