Question

The strength of paper used in the manufacturing of cardboard boxes (y) is related to percentage of hardwood concentration in the original pulp (x). Under controlled conditions, a pilot plant manufactures 16 samples, each from differential batch of pulp, and measures the tensile strength. Determine if there is significance relationship between x and y.

y = 101, 117, 117, 106, 132, 147, 147, 134, 111, 123, 125, 145, 134, 145, 144, 146.9
x = 1.0, 1.5, 1.5, 1.5, 2.0, 2.0, 2.2, 2.4, 2.5, 2.5, 2.8, 2.8, 3.0, 3.0, 3.2, 3.3

Answer 1

At a significance level of 0.05, there is enough evidence to claim that there is a significant relationship between x and y.

P-value = 0.003.

Explanation:

If we perform a regression analysis relating x and y, we get the best fitting line with equation:

`y=15.82x+92.9`

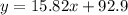
and a correlation coefficient r:

`r=0.693`

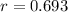
We have to test the hypothesis, where the alternative hypothesis claims that there is a relationship between these two variables, and the null hypothesis claiming there is no relationship (meaning that the correlation is not significantly different from 0).

This can be written as:

`H_0: \rho=0\\\\H_a:\rho\\eq0`

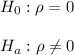
where ρ is the population correlation coefficient for x and y.

The significance level is assumed to be 0.05.

The sample size is n=16.

The degrees of freedom are df=14.

`df=n-2=16-2=14`

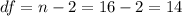
The test statistic can be calculated as:

`t=(r√(n-2))/(√(1-r^2))=(0.693√(14))/(√(1-(0.693)^2))=(2.593)/(0.721)=3.597`

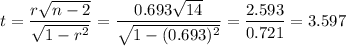
For a test statistic t=2.05 and 14 degrees of freedom, the P-value is calculated as:

`\text{P-value}=2\cdot P(t>3.597)=0.003`

The P-value (0.003) is smaller than the significance level (0.05), so the effect is significant enough.

The null hypothesis is rejected.

At a significance level of 0.05, there is enough evidence to claim that there is a significant relationship between x and y.