Answer:
the amount of force needed to hold the nozzle is 1100 N
Step-by-step explanation:
Given that;
The diameter of the fire horse is 7.0cm
The radius of the fire horse is d/2 = 7.0/2 = 3.5 cm = 0.035 m
the water running through the hose flows at 420 L/min = 0.42 m³/ 60 sec
The diameter of the nozzle = 0.75 cm
The radius of the nozzle = d/2 = 0.75/2 = 0.375 cm = 0.00375 m
Amount of force needed to hold the nozzle = ??
Using equation of continuity product
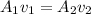
where
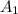 = cross sectional area of the hose
= cross sectional area of the hose
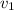 = velocity of water flow at hose
= velocity of water flow at hose
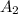 = cross sectional area of the nozzle
= cross sectional area of the nozzle
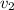 = velocity of water flow at nozzle
= velocity of water flow at nozzle
Making
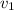 the subject of the formula; we have
the subject of the formula; we have
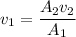
Also making
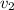 the subject of the formula:
the subject of the formula:
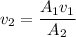
Also; from newton's law; we all know that F = ma
where ;
m = mass
a = acceleration
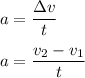
So ;
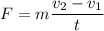
Also ; mass = density × volume
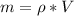
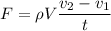
![F = (\rho V)/(t)[ (A_1v_1)/(A_2)- (A_2v_2)/(A_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/ck1lhcwsenzuo19mz5pxf2is3cawmunlur.png)
Replacing
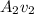 by
by
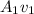 from above ; so
from above ; so
![F = (\rho V)/(t)[ (A_1v_1)/(A_2)- (A_1v_1)/(A_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/3h8f5a6ulkwto4ho2sdp732soxpxgdtjex.png)
![F = (\rho V)/(t) A_1 v_1 [ (1)/(A_2)- (1)/(A_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/9ckhq6sqjcet9yj65e2ab59m3kryo4a0n4.png)
where the product of cross section area of velocity is equal to the volume of water and its time flow;
SO;
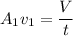
Replacing that into what we have above; we have:
![F = (\rho V)/(t) (V)/(t) [ (1)/(A_2)- (1)/(A_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/nud8qi64su7ydldoxi4if8j7gjf6d6dmwh.png)
![F ={\rho }( (V)/(t))^2 [ (1)/(A_2)- (1)/(A_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/2x71n2vvsig9pdszel86m83apqjnut3mxt.png)
Where;
A = πr²
![F ={\rho }( (V)/(t))^2 [ (1)/(\pi r^2_2)- (1)/(\pi r^2_1)]](https://img.qammunity.org/2021/formulas/physics/high-school/yednkissrtlsexplu03mibbj1n4ug2jw39.png)
![F ={(1000*10^3 \ kg/m^3) }( (0.42 m^3 )/(60 sec))^2 [ (1)/(\pi (0.00375)^2)- (1)/(\pi (0.035)^2)]](https://img.qammunity.org/2021/formulas/physics/high-school/5qqzouzgag24isghe8m804j4cnxq0l1ar9.png)
F = 1100 N
Thus; the amount of force needed to hold the nozzle is 1100 N