Question

g Gravel is being dumped from a conveyor belt at a rate of 10 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 6 ft high

Answer 1

0.3537 feet per minute.

Explanation:

Gravel is being dumped from a conveyor belt at a rate of 10 ft3/min. Since we are told that the shape formed is a cone, the rate of change of the volume of the cone.

`(dV)/(dt)=10$ ft^3/min`

`\text{Volume of a cone}=(1)/(3)\pi r^2 h`

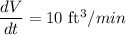
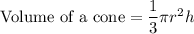
If the Base Diameter = Height of the Cone

The radius of the Cone = h/2

Therefore,

`\text{Volume of the cone}=(\pi h)/(3) ((h)/(2)) ^2 \\V=(\pi h^3)/(12)`

`\text{Rate of Change of the Volume}, (dV)/(dt)=(3\pi h^2)/(12)(dh)/(dt)`

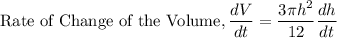
Therefore:
`(3\pi h^2)/(12)(dh)/(dt)=10`

We want to determine how fast is the height of the pile is increasing when the pile is 6 feet high.

`When h=6$ feet$\\(3\pi *6^2)/(12)(dh)/(dt)=10\\9\pi (dh)/(dt)=10\\ (dh)/(dt)= (10)/(9\pi)\\ (dh)/(dt)=0.3537$ feet per minute`

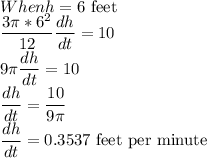
When the pile is 6 feet high, the height of the pile is increasing at a rate of 0.3537 feet per minute.