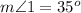Question

M(angle)1 =. Degrees

Answer 1

Angle
`m\angle 1 = 35^o`

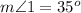
Explanation:

Our goal is to find appropriate symmetries within the given diagram, so we can use the property of the addition of internal angles of a triangle that render
`180^o`.

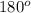So we start by drawing a line that goes through the center of the circle and also through the vertex of angle
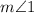`m\angle 1`. Please see the attached image to follow the procedure. In the image, the line is a fine black line that crosses the circle completely.

Now we draw the four radii that will define clearly the central angles of
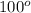`100^o` and
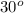`30^o` that come as information.

Then we set our efforts to analyze the two triangles (one marked with green borders, and the other one marked with orange borders. Notice that the angle on the further right for the triangle with orange borders is in fact half of the angle
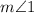`m\angle 1` that we need to find, so we will work our way to determine the size of it and then multiply it by two.

We need to start though with the triangle with green borders because it has more information that we can derive.

Notice that this green triangle has a central angle equal to
`115^o`, because it has to measure the same as 180 degrees minus half of the 100 degrees angle and minus half of the 30 degree angle in order to add to form the perfect plane angle of the circle's diameter:

`180^o-50^o-15^o=115^o`

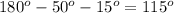
Now, notice as well that this green triangle is an isosceles triangle (has two equal sides (both equal to the radius of the circle), and therefore the angles opposite to them must be equal. We can find the measure of either such angles by using the property of additions of internal angles of a triangle to render
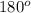`180^o`, subtracting from it the 115 degree angle we know, and dividing the result by two:

`180^o-115^o=65^o`

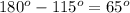
half of this is
`32.5^o`

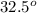
Now we use this angle, to find its supplementary angle, which would be the angle on top of the orange triangle:

`180^o-32.5^o=147.5^o`

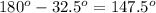
Now all we need is to use the property of addition of internal angles for the orange triangle (of which we currently know a 15 degree angle and a 147.5 degree angle) to find what half of angle
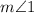`m\angle 1` is:

`180^o-147.5^o-15^o=17.5^o`

then angle
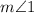`m\angle 1` is twice this value:
`m\angle 1 = 35^o`