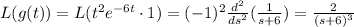Question

Laplace Transform Let f be a function defined for t ≥ 0. Then the integral ℒ{f(t)} = [infinity] e−stf(t) dt 0 is said to be the Laplace transform of f, provided that the integral converges. to find ℒ{f(t)}. (Write your answer as a function of s.) f(t) = t2e−6t

Answer 1

The laplace transform is
`(2)/((s+6)^3)`

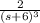
Explanation:

We will solve this problem by applying the laplace transform properties (their proofs are beyond the scope of this explanation).

Consider first the function f(t) = 1. By definition of the laplace transform, we have

`F(s) = \int_(0)^(\infty)f(t)e^(-st)dt`

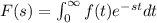
when f(t) = 1 we get

`F(s) = \int_(0)^(\infty)e^(-st)dt = \left.(-e^(-st))/(s)\right|_(0)^(\infty) = (1)/(s)`

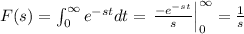
We will apply the following properties: Define L(f) as applying the laplace transform

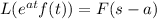`L(e^(at)f(t)) = F(s-a)` (this means, multiplying by an exponential corresponds to a shift in the s parameter of the transform of f)

`L(t^nf(t)) = (-1)^n(d^n F)/(ds^n)` (this is, multypling by
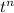`t^n` is equivalent to taking the n-th derivative of the transform.

We are given the function
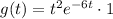`g(t) = t^2e^(-6t)\cdot 1`. Since the transform of the constant function 1 is 1/s, by applying the first property we get

`L(e^(-6t)\cdot 1 ) = (1)/(s+6)`

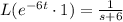
By applying the second property we get

`L(g(t)) = L(t^2 e^(-6t) \cdot 1) = (-1)^2(d^2)/(ds^2)((1)/(s+6)) = (2)/((s+6)^3)`