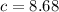Question

Problem PageQuestion Calcium levels in people are normally distributed with a mean of mg/dL and a standard deviation of mg/dL. Individuals with calcium levels in the bottom of the population are considered to have low calcium levels. Find the calcium level that is the borderline between low calcium levels and those not considered low. Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The calcium level that is the borderline between low calcium levels and those not considered low is
`c = 8.68`

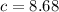
Explanation:

From the question we are told that

The mean is
`\mu = 9.5\ mg/dL`

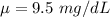
The standard deviation
`\sigma = 0.5 \ mg/dL`

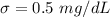
The proportion of the population with low calcium level is
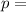`p =`5% = 0.05

Let X be a X random calcium level

Now the P(X < c) = 0.05

Here P denotes probability

c is population with calcium level at the borderline

Since the calcium level is normally distributed the z-value is evaluated as

`P(Z < (c - \mu)/(\sigma ) ) = 0.05`

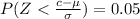
The critical value for 0.05 from the standard normal distribution table is

`t_(0.05) = -1.645`

=>
`(c - \mu)/(\sigma ) = -1.645`

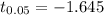
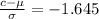
substituting values

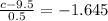
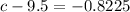
`(c - 9.5)/(0.5 ) = -1.645`

=>
`c - 9.5 = -0.8225`

=>
`c = 8.68`