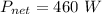Question

In this problem you will consider the balance of thermal energy radiated and absorbed by a person.Assume that the person is wearing only a skimpy bathing suit of negligible area. As a rough approximation, the area of a human body may be considered to be that of the sides of a cylinder of length L=2.0m and circumference C=0.8m.For the Stefan-Boltzmann constant use σ=5.67×10−8W/m2/K4.Part aIf the surface temperature of the skin is taken to be Tbody=30∘C, how much thermal power Prb does the body described in the introduction radiate?Take the emissivity to be e=0.6.Express the power radiated into the room by the body numerically, rounded to the nearest 10 W.part bFind Pnet, the net power radiated by the person when in a room with temperature Troom=20∘C

Answer 1

The thermal power emitted by the body is
`P_t = 286.8 \ Wm^(-2)`

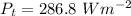
The net power radiated is
`P_(net) = 460 \ W`

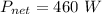
Step-by-step explanation:

From the question we are told that

The length of the assumed hum
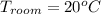`T_(room) = 20 ^oC`an body is L = 2.0 m

The circumference of the assumed human body is
`C = 0.8 \ m`

The Stefan-Boltzmann constant is
`\sigma = 5.67 * 10^(-8 ) \ W\cdot m^(-2) \cdot K^(-4).`

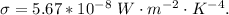
The temperature of skin
`T_(body) = 30^oC`

The temperature of the room is

The emissivity is e=0.6

The thermal power radiated by the body is mathematically represented as

`P_t = e * \sigma * T_(body)^4`

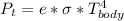
substituting value

`P_t = 0.6 * 5.67*10^(-8) * (303)^4`

`P_t = 286.8 \ Wm^(-2)`

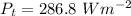
The net power radiated by the body is mathematically evaluated as

`P_(net) = P_t * A`

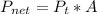
Where A is the surface area of the body which is mathematically evaluated as

`A = C* L`

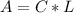
substituting values

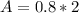
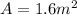
`A = 0.8 * 2`

`A = 1.6 m^2`

=>
`P_(net) = 286.8 * 1.6`

=>
`P_(net) = 460 \ W`