Question

A six-foot-tall basketball player shoots a ball towards the basket and misses. The height in feet of the ball up off the floor of the court as it travels through the air can be modeled by the function:
`h(x)=-16x^2+48x+6` where x is the number of seconds the ball is in the air after the shot is taken. When does the ball reach its maximum height? What is the maximum height of the ball? How much time will pass in seconds from the start of the shot to the ball hitting the floor? Answer all three questions to receive full credit.

Answer 1

i) The maximum height of the ball 'x' = 1.5 seconds

ii) The maximum height = 42

Explanation:

Step(i):-

Given h(x) = - 16 x² + 48 x +6 ...(i)

Differentiating equation (i) with respective to 'x'

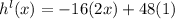`h ^(l) (x) = - 16 (2 x) +48 (1)` ...(ii)

Equating Zero

- 3 2 x + 4 8 = 0

- 32 x = - 48

x = 1.5

step(ii):-

The maximum height of the ball 'x' = 1.5

Again Differentiating equation (ii) with respective to 'x'

`h ^(ll) (x) = - 16 (2 x) < 0`

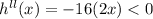
The maximum height 'x' = 1.5

h(x) = - 16 x² + 48 x +6

h(1.5) = - 16 (1.5)² +4 8 (1.5) +6

= 42

The maximum height at x = 1.5 is = 42

Final answer:-

i) The maximum height of the ball 'x' = 1.5 seconds

ii) The maximum height = 42