Answer:

Step by step Explanation'
To solve this problem, we will need to apply trial-and-error calculation with the binomial distribution, even though it appears like Central Limit Theorem but it's not.
For us to know the value of C , we will look for a minimum integer such that having 'n' number of high performance level of employee has the probability below 0.01.
Determine the maximum value of C, then the maximum value that C can have is 120/n
Let us represent X as the number of employees with high performance with a binomial distribution of
P =0.02( since the percentage of chance of achieving a high performance level is 2%)
n = 20 ( number of employees who achieve a high performance level)
The probability of X= 0 can be calculated
P( X= 0) = 0.98^n
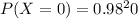
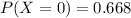

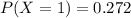
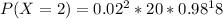
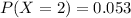
Summation of P( X= 0)+ P( X= 1)+P( X= 2) will give us the value of 0.993 which is greater than 0.99( 1% that the fund will be inadequate to cover all payments for high performance.)
BUT the summation of P( X= 0)+ P( X= 1) will give the value of 0.94 which doesn't exceed the 0.99 value,
Therefore, the minimum value of integer in such a way that P(X >2) is less than 0.01 have n= 2
then the maximum value that C can have is 120/n
