Answer:
Explanation:
Hello!
The claim is that the variability of the output levels of the night-shift is greater than the variability in the output levels of the day workers.
Be
X₁: output level of night shift workers.
n₁= 9
X[bar]₁= 520
S₁= 38
X₂: output level of day shift workers.
n₂= 8
X[bar]₂= 540
S₂= 20
Considering both variables have a normal distribution, the parameters of interest are the population variances.
a)
H₀: σ₁² ≤ σ₂²
H₁: σ₁² > σ₂²
b)
To compare both variances you have to conduct a variance ratio test with statistic:
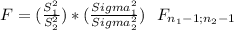
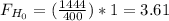
c)
The test is one tailed to the right, the p-value will have the same direction, i.e. it will be in the right tail of the distribution. The F distribution has degrees of freedom:
n₁ - 1= 9 - 1= 8
n₂ - 1= 8 - 1= 7
P(F₈,₇ ≥ 3.61) = 1 - P(F₈,₇ < 3.61) = 1 - 0.9461= 0.0539
The p-value of this test is 0.0539
d)
The CI for the variance ratio is:
![[(S^2_1/S_2^2)/(F_(n_1-1;n_2-1;1-\alpha /2)); (S^2_1/S_2^2)/(F_(n_1-1;n_2-1;\alpha /2))]](https://img.qammunity.org/2021/formulas/mathematics/college/p0s73htyf2eagsar65ol9yrmx0vy5pcos4.png)
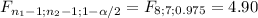
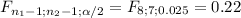
![[(1444/400)/(4.90)}; (1444/400)/(0.22)}]](https://img.qammunity.org/2021/formulas/mathematics/college/8th2fzk5lnvphplws9edsu1jqkfubm19b5.png)
[0.736; 16.409]
Using the level of significance complementary to the confidence level of the interval, you can compare it to the p-value calculated in item c.
p-value: 0.0539
α: 0.05
The p-value is less than the significance level, the decision is to reject the null hypothesis. Using a 5% significance level you can conclude that the variance in the output levels of the night shift workers is greater than the variance in the output levels of the day shift workers.