Question

(d) A drinks machine dispenses coffee into cups. A sign on the machine indicates that each cup contains 100ml of coffee. The machine actually dispenses a mean amount of 105ml per cup and 10% of the cups contain less than the amount stated on the sign. Assuming that the amount of coffee dispenses into each cup is normally distributed, find the standard deviation of the amount of coffee dispensed per cup in ml.

Answer 1

The standard deviation of the amount of coffee dispensed per cup in ml is 3.91.

Explanation:

Let the random variable X denote the amount of coffee dispensed by the machine.

It is provided that the random variable, X is normally distributed with mean, μ = 105 ml/cup and standard deviation, σ.

It is also provided that a sign on the machine indicates that each cup contains 100 ml of coffee.

And 10% of the cups contain less than the amount stated on the sign.

To compute the probabilities of a normally distributed random variable, first convert the raw score to a z-score,

`z=(X-\mu)/(\sigma)`

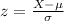
This implies that:

P (X < 100) = 0.10

⇒ P (Z < z) = 0.10

The value of z for the above probability is, z = -1.28.

*Use a z-table

Compute the value of standard deviation as follows:

`z=(X-\mu)/(\sigma)`

`-1.28=(100-105)/(\sigma)`

`\sigma=(-5)/(-1.28)`

`=3.90625\\\\\approx 3.91`

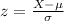
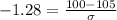
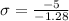
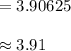
Thus, the standard deviation of the amount of coffee dispensed per cup in ml is 3.91.