Question

In the given figure ABCD is a parallelogram, E is the midpoint of BC. DE produced meets AB produced at L. Prove that AB = B L and AL=2DC​

Answer 1

See Reasoning Below

Explanation:

To prove that AB = BL, or in other words AB ≅ BL, let us consider the triangles CED and BEL. If we were to prove they were congruent, then by CPCTC ( corresponding parts of congruent triangle are congruent ) DC ≅ BL. As AB ≅ DC by " Properties of Parallelogram " it would be that through transitivity, AB ≅ BL / AB = BL;

`m<CED = m<BEL,\\BE = CE,\\m< DCE = LBE\\\\\\CED = BEL,\\DC = BL,\\AB = BL - Proved`

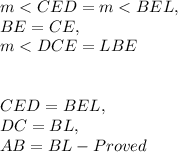
Now for " part 2 " we can consider that AB = DC, from part 1. If AB = BL, then AL = 2 ( AB ) by the Partition Postulate. AB = DC, so we can also say that AL = 2 ( DC ) - Proved

See attachment in statement reasoning form for part 1;