Answer:
The 90% confidence interval for the difference in mean number of days meeting the goal is (4.49, 18.11).
Explanation:
The (1 - α)% confidence interval for the difference between two means is:
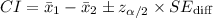
It is provided that:
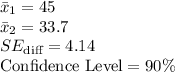
The critical value of z for 90% confidence level is,
z = 1.645
*Use a z-table.
Compute the 90% confidence interval for the difference in mean number of days meeting the goal as follows:
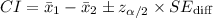

Thus, the 90% confidence interval for the difference in mean number of days meeting the goal is (4.49, 18.11).