Answer:


The correct answer choice is a. (62.2, 113.8)
Explanation:
Of the 500 customers who were told the increase applied to charges above $1000 each month, the average increase in spending was $527 with a standard deviation of $225.
Sample size = n₁ = 500
Sample mean = x₁ = $527
Standard deviation = s₁ = $225
Of the 500 customers who were told the increase applied to charges above $2000 each month, the average increase in spending was $439 with a standard deviation of $189
Sample size = n₂ = 500
Sample mean = x₂ = $439
Standard deviation = s₂ = $189
We are asked to find the 95% confidence interval for the difference between two means.
The given group of answer choices are
a. (62.2, 113.8)
b. (86.2, 120.5)
c. (10.3, 23.8)
d. (55.6, 67.8)
The confidence interval for the difference between two means is given by

Where
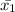 and
and
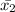 are the given sample means and margin of error is given by
are the given sample means and margin of error is given by
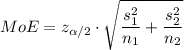
The z-score corresponding to 95% confidence level is given by
Significance level = α = 1 - 0.95 = 0.05/2 = 0.025
From the z-table at α = 0.025 the z-score is 1.96
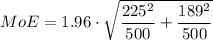
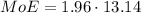
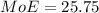
Finally,


Therefore, the correct answer choice is a. (62.2, 113.8)
How to use z-table?
In the z-table find the probability of 0.025
Note down the value of that row, it would be 1.9.
Note down the value of that column, it would be 0.06.
Add the two numbers together.
The z-score is 1.9 + 0.06 = 1.96