Answer:
The probability that both the male and female student are non-smokers is 0.72.
Explanation:
The complete question is:
At a local college,178 of the male students are smokers and 712 are non-smokers. Of the female students,80 are smokers and 720 are nonsmokers. A male student and a female student from the college are randomly selected for a survey. What is the probability that both are non-smokers?
Solution:
Let, X denote the number of non-smoker male students and Y denote the number of non-smoker female students.
It is provided that:
X' = 178
X = 712
Tx = 890
Y' = 80
Y = 720
Ty = 800
Compute the probability of selecting a non-smoker male student as follows:
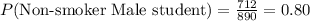
Compute the probability of selecting a non-smoker female student as follows:
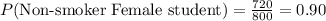
Compute the probability that both the male and female student are non-smokers as follows:
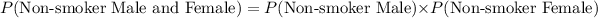 The event of any female student being a non-smoker is independent of the male students.
The event of any female student being a non-smoker is independent of the male students.
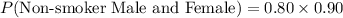
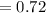
Thus, the probability that both the male and female student are non-smokers is 0.72.