Question

A 20 g "bouncy ball" is dropped from a height of 1.8 m. It rebounds from the ground with 80% of the speed it had just before it hit the ground. Assume that during the bounce the ground causes a constant force on the ball for 75 ms. What is the force applied to the ball by the ground in N?

The following are not correct: 0.513 N, 0.317 N, 0.121 N. Please show your work so I can understand!

Answer 1

F = 0.314 N

Step-by-step explanation:

In order to calculate the applied force to the ball by the ground, you first calculate the speed of the ball just before it hits the ground. You use the following formula:

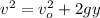`v^2=v_o^2+2gy` (1)

y: height from the ball starts its motion = 1.8 m

vo: initial velocity = 0 m/s

g: gravitational acceleration = 9.8 m/s^2

v: final velocity of the ball = ?

You replace the values of the parameters in the equation (1):

`v=√(2gy)=√(2(9.8m/s^2)(1.8m))=5.93(m)/(s)`

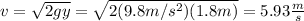
Next, you take into account that the force exerted by the ground on the ball is given by the change, on time, of the linear momentum of the ball, that is:

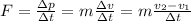`F=(\Delta p)/(\Delta t)=m(\Delta v)/(\Delta t)=m(v_2-v_1)/(\Delta t)` (2)

m: mass of the ball = 20g = 20*10^-3 kg

v1: velocity of the ball just before it hits the ground = 5.93m/s

v2: velocity of the ball after it impacts the ground (80% of v1):

0.8(5.93m/s) = 4.75 m/s

Δt: time interval o which the ground applies the force on the ball = 75*10^-3 s

You replace the values of the parameters in the equation (2):

`F=(20*10^(-3)kg)(4.75m/s-5.93m/s)/(75*10^(-3)s)=-0.314N`

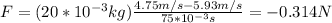
The minus sign means that the force is applied against the initial direction of the motion of the ball.

The applied force by the ground on the bouncy ball is 0.314 N