Question

During a baseball game, a baseball is struck at ground level by a batter. The ball leaves the baseball bat with an initial speed v0 = 38 m/s at an angle θ = 35° above horizontal. Let the origin of the Cartesian coordinate system be the ball's position the instant it leaves the bat. Air resistance may be ignored throughout this problem.

Part (a) Express the magnitude of the ball's initial horizontal velocity Or in terms of vo and 20%
Part (b) Express the magnitude of the ball's initial vertical velocity vOy in terms of vo and 0. 20%
Part (c) Find the ball's maximum vertical height Amat in meters above the ground.
Part (d) Create an expression in terms of vo-e, and g for the time-ur İt takes te ball to travel to its maximum vertical height.
Part (e) Calculate the horizontal distance in meters the ball has traveled when it returns to ground level.

Answer 1

a) v₀ₓ = v₀ cos θ , b) v_{oy} = v₀ sin θ , c) y = v_{oy}² / 2g, y = 24.25 m

e) R = 138.46 m

Step-by-step explanation:

This is a projectile launch exercise

a) let's use trigonometry to find the components of the initial velocity

cos θ = v₀ₓ / v₀

v₀ₓ = v₀ cos θ

v₀ₓ = 38 cos 35

v₀ₓ = 31.13 m / s

b) sin θ =
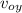`v_(oy)` / v₀

v_{oy} = v₀ sin θ

v_{oy} = 38 sint 35

v_{oy} = 21 80 m / s

c, d) to find the maximum height, the vertical speed is zero

v_{y}² = v_{oy}² - 2 g y

0 =
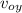`v_(oy)`² - 2 gy

y = v_{oy}² / 2g

let's calculate

y = 21.80 2 / (2 9.8)

y = 24.25 m

e) They ask to find the horizontal distance

for this we can use the expression of reaches

R = v₀² sin 2θ / g

let's calculate

R = 38² sin (2 35) / 9.8

R = 138.46 m