Question

A baseball is thrown into the air from a height of 5 feet. The ball reaches a maximum height of 43.5 feet and spends a total of 3.2 seconds in the air. Which equation models the height of the baseball? Assume that acceleration due to gravity is –16 ft/s2.

Answer 1

Explanation:

Since we know that the max height is 43.5 feet, we can use that in the work form of a parabola to solve for the time it was at its max height. This time will serve as the h value in the vertex of the parabola. Then we can rewrite the parabola in terms of time.

The work form of a parabola is

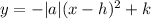`y=-|a|(x-h)^2+k` and believe it or not, we have everything we need to solve for h. We know the k of the vertex (43.5) and we also know that at time 0, before any time at all went by, the object started out at 5 feet. So we have a coordinate to use (0, 5) as x and y. We also know that a = 16. Plugging all that in to the work form:

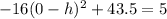`-16(0-h)^2+43.5=5` and

`-16(h^2)=-38.5` and

`h^2=2.40625` so

h = 1.551209206 sec

This gives us a vertex of (1.551209206, 43.5).

Now let's plug in and find the rest of the equation.

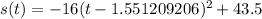`s(t)=-16(t-1.551209206)^2+43.5` and expanding that binomial:

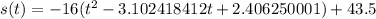`s(t)=-16(t^2-3.102418412t+2.406250001)+43.5` and distributing the -16 in:

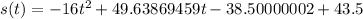`s(t)=-16t^2+49.63869459t-38.50000002+43.5` and combining like terms:

`s(t)=-16t^2+49.63869459t+4.9999999`

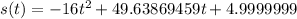
so if we round to the nearest whole number, the quadratic will be

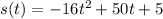`s(t)=-16t^2+50t+5` which tells us that this object was lauched from an initial height of 5 feet and that it was launched at an upward velocity of 50 feet/sec.