Question

Benny is trying to learn how to ride a bike, but is terrified of falling. He did some research, and discovered that if he rides a bike with training wheels, the probability of falling is 0.1; if he learns to ride a bike by using a bike without training wheels, his probability of falling is 0.5, and if he uses a unicycle, his probability of falling is 0.8. Benny came home crying with a bruise on his knee, after falling. His mom is trying to guess how Benny was trying to learn to ride a bike.

a) Assuming that the probability that Benny was using each of these 3 methods is equal, what is the probability that Benny was learning to ride a bike using the training wheels?
b) Since Benny's mom knows Benny so well, she knows that the probability that he was using training wheels is 0.7, regular bike is 0.2, and unicycle is 0.1. What is the probability now that Benny fell while using the training wheels?

Answer 1

a) 7.14% probability that Benny was learning to ride a bike using the training wheels

b) 28% probability that Benny was learning to ride a bike using the training wheels

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

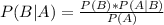
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

Benny came home crying with a bruise on his knee, after falling. His mom is trying to guess how Benny was trying to learn to ride a bike.

a) Assuming that the probability that Benny was using each of these 3 methods is equal, what is the probability that Benny was learning to ride a bike using the training wheels?

So

Event A: Benny fell

Event B: Benny was using training wheels.

The probability that Benny was using each of these 3 methods is equal

This means that
`P(B) = (1)/(3)`

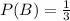
He did some research, and discovered that if he rides a bike with training wheels, the probability of falling is 0.1;

This means that
`P(A|B) = 0.1`

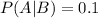
Probability of falling:

1/3 of the time, he uses training wheels. With training wheels, the probability of falling is 0.1.

1/3 of the time, he uses the bike without training wheels. Without training wheels, the probability of falling is 0.5

1/3 of the time, he uses the unicycle, for which he has an 0.8 probability of falling. Then

`P(A) = (0.1 + 0.5 + 0.8)/(3) = 0.4667`

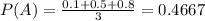
So

`P(B|A) = ((1)/(3)*0.1)/(0.4667) = 0.0714`

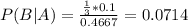
7.14% probability that Benny was learning to ride a bike using the training wheels

b) Since Benny's mom knows Benny so well, she knows that the probability that he was using training wheels is 0.7, regular bike is 0.2, and unicycle is 0.1. What is the probability now that Benny fell while using the training wheels?

Similar as above, just some probabilities change.

Event A: Benny fell

Event B: Benny was using training wheels.

The probability that he was using training wheels is 0.7

This means that
`P(B) = 0.7`

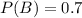
He did some research, and discovered that if he rides a bike with training wheels, the probability of falling is 0.1;

This means that
`P(A|B) = 0.1`

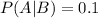
Probability of falling:

0.7 of the time, he uses training wheels. With training wheels, the probability of falling is 0.1.

0.2 of the time, he uses the bike without training wheels. Without training wheels, the probability of falling is 0.5

0.1 of the time, he uses the unicycle, for which he has an 0.8 probability of falling. Then

`P(A) = 0.7*0.1 + 0.2*0.5 + 0.1*0.8 = 0.25`

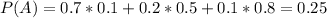
So

`P(B|A) = (0.7*0.1)/(0.25) = 0.28`

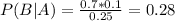
28% probability that Benny was learning to ride a bike using the training wheels