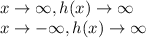Question

The end behaviour for the polynomial function h(x)=−x3+x4−2x+1 h ( x ) = - x 3 + x 4 - 2 x + 1 is: x→−[infinity], y→−[infinity] x → - [infinity] , y → - [infinity] and x→[infinity], y→[infinity] x → [infinity] , y → [infinity] x→−[infinity], y→[infinity] x → - [infinity] , y → [infinity] and x→[infinity], y→[infinity] x → [infinity] , y → [infinity] x→−[infinity], y→−[infinity] x → - [infinity] , y → - [infinity] and x→[infinity], y→−[infinity] x → [infinity] , y → - [infinity] Unable to tell.

Answer 1

`\text{As } x \to \infty, y \to \infty,$and as x \to -\infty, y \to \infty`

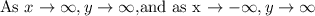
Explanation:

Given the polynomial function:
`h(x)=-x^3+x^4-2x+1`

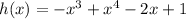
To examine its end behavior, we create a table of values that we can then examine.

`\left|\begin{array}cx&h(x)\\--&--\\-4&329\\-3&115\\-2&29\\-1&5\\0&1\\1&-1\\2&5\\3&49\\4&185\end{array}\right|`

From the table, we see a repeating pattern of positive values of h(x) with h(1)=-1 being an axis of symmetry.

Therefore, as:

`x \to \infty, h(x) \to \infty\\x \to -\infty, h(x) \to \infty`