Question

The roof of a house consists of a 22-cm-thick concrete slab (k = 2 W/m•K) that is 15 m wide and 20 m long. The emissivity of the outer surface of the iroof is 0.9, and the convection heat transfer coefficient on that surface is estimated to be 15 W/m2•K The inner surface of the roof is maintained at 15°C. On a clear winter night, the ambient air is reported to be at 10°C while the night sky temperature for radiation heat transfer is 255 K. Considering both radiation and convection heat transfer, determine the outer surface temperature and the rate of heat transfer through the roof. if the house is heated by a furnace burning natural gas with an efficiency of 85 percent, and the unit cost of natural gas is 51.20/therm (1 therm = 105.500 U of energy content), determine the money lost through the roof that night during a 14-hour period.

Answer 1

Step-by-step explanation:

Consider the outer surface of the roof to be
`T_(out)`

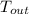
Since, the heat conducted is equal to the sum of the heat transferred through convection and the rest by radiation

`Q_(cond)=Q_(rad)+Q_(conv)`

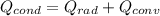
Rewrite the equation as follows

`kA_s(\Delta T)/(L) =\epsilon \sigma A_s(T_s^4-T_(\infty)^4)+hA_s \Delta T\\\\k(\Delta T)/(L) =\epsilon \sigma (T_s^4-T_(\infty)^4)+h \Delta T`

`k(T_(in)-T_(out))/(L) =\epsilon \sigma (T_(out)^4-T_(rad)^4)+h(T_(out)-T_(\infty))`

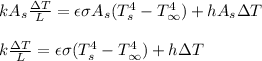
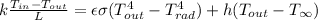
subsititute

k = 2 W/m

`15^o C=T_(in)`

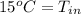
0.22 for L

`0.9 = \epsilon`

`5.67* 10^(-8)W/m^2.K^4=\sigma`

`255=T_(rad)`

`15W/m^2.K = h`

`10^oC=T_(\infty)`

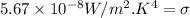
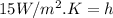
`2* (15 -T_(out))/(0.22) =[0.9*(5.67*10^-^8)*((T_(out)+273)^4-255^4)]+[15*(T_(out)-10)]\\\\T_(out)=7.7^oC`

Hence, the temperature of outer surface of the roof is
`T_(out)=7.7^oC`

Calculate the surface area of the roof

`A_s=b* l`

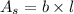
Here, b is the width , l is the length

substitute 15 for b , 20 for l

`A_s=15 * 20\\\\=300m^2`

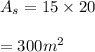
Write the equation for conduction

`Q_(cond)=kA_s(\Delta T)/(L)`

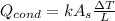
substitute 2W/m.K for k

`300m^2 \ \ for \ A_s\\\\(15-7.7)^oC \ \ for \ \Delta T\\\\0.22m \ for \ L`

`Q_(cond)=2* 300 * (15-7.7)/(0.22)\\\\=19,000`

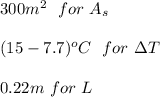
Therefore, the total heat transferred through conduction is
`Q_(cond)=19,9009W`

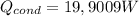
Consider the amount of natural gas required be R and the cost incurred in running the furnace through the night be M

`R=(Q_(cond))/(0.85) * T`

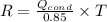
Duration of time T = 14 x 3600s

`R=(19909*(14*3600))/(0.85)kJ\\\\= (19909*(14*3600))/(0.85*105500)therm\\\\=11.2 \ therm`

And the required money for the gas M = 11.2 x $1.2

= $13.44

Therefore, the money lost through the roof due to the heat transfer M=$13.44