Question

A study was performed on green sea turtles inhabiting a certain area.​ Time-depth recorders were deployed on 6 of the 76 captured turtles. The​ time-depth recorders allowed the environmentalists to track the movement of the sea turtles in the area. These 6 turtles had a mean shell length of 51.3 cm and a standard deviation of 6.6 cm. Complete parts a and b below.

1. Use the information on the 6 tracked turtles to estimate, with 99% confidence, the true mean shell length of all green sea turtles in the area. (Round to one decimal place as needed.) Interpret the result.
Choose the correct answer below.
A. One can be 99% confident the true mean shell length lies at the mean of the above interval.
B. One can be 99% confident the true mean shell length is one of the end points of the above interval.
C. One can be 99% confident the true mean shell length lies within the above interval.
D. There is a 99% probability that the true mean shell length is the mean of the interval.
What assumption about the distribution of shell lengths must be true in order for the confidence interval, part a, to be valid?
A. The population has a relative frequency distribution that is approximately exponential.
B. The population has a relative frequency distribution that is approximately uniform.
C. The population has a relative frequency distribution that is approximately normal.
D. The population has a relative frequency distribution that is approximately binomial.
2. Is this assumption reasonably satisfied? Use the accompanying data for all 76 turtles to help answer this question. Choose the correct answer below.
A. No
B. Yes

Answer 1

One can be 99% confident the true mean shell length lies within the above interval.

The population has a relative frequency distribution that is approximately normal.

Explanation:

We are given that Time-depth recorders were deployed on 6 of the 76 captured turtles. These 6 turtles had a mean shell length of 51.3 cm and a standard deviation of 6.6 cm.

The pivotal quantity for a 99% confidence interval for the true mean shell length is given by;

P.Q. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean shell length = 51.3 cm

s = sample standard deviation = 6.6 cm

n = sample of turtles = 6

`\mu` = true mean shell length

Now, the 99% confidence interval for
`\mu` =
`\bar X \pm t_(_(\alpha)/(2)_) * (s)/(√(n) )`

Here,
`\alpha` = 1% so
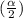`((\alpha)/(2))` = 0.5%. So, the critical value of t at 0.5% significance level and 5 (6-1) degree of freedom is 4.032.

So, 99% confidence interval for
`\mu` =
`51.3 \pm 4.032 * (6.6)/(√(6) )`

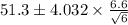
= [51.3 - 10.864 , 51.3 + 10.864]

= [40.44 cm, 62.16 cm]

The interpretation of the above result is that we are 99% confident that the true mean shell length lie within the above interval of [40.44 cm, 62.16 cm].

The assumption about the distribution of shell lengths must be true in order for the confidence interval, part a, to be valid is that;

C. The population has a relative frequency distribution that is approximately normal.

This assumption is reasonably satisfied as the data comes from the whole 76 turtles and also we don't know about population standard deviation.