Question

Playbill magazine reported that the mean annual household income of its readers is $119,155 (Playbill, January 2006). Assume this estimate of the mean annual household in- come is based on a sample of 80 households, and based on past studies, the population standard deviation is known to be a = $30,000. a. Develop a 90% confidence interval estimate of the population mean. b. Develop a 95% confidence interval estimate of the population mean. c. Develop a 99% confidence interval estimate of the population mean. d. Discuss what happens to the width of the confidence interval as the confidence level is increased. Does this result seem reasonable? Explain.

Answer 1

a) CI = (113,637.5 , 124,672.5)

b) CI = (112,581 , 125,729)

c) CI = (110,501.4 , 127,808.6)

Explanation:

You have the following information:

`\overline{x}`: mean annual household income = 119,155

σ: standard deviation = 30,000

n: sample = 80

The interval of confidence is given by the following expression:

`\overline{x}\pm Z_(\alpha/s)((\sigma)/(√(n)))`

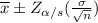
Z_α/2: distribution density factor

where α and Z_α/2 are given by the range of the confidence interval.

a) For a 90% confidence interval you have:

α = 1 - 0.9 = 0.1

Z_0.1/2 = Z_0.05 = 1.645 (found in a table of normal distribution)

You replace in the equation (1) to obtain the confidence interval:

`119,155\pm (1.645)((30,000)/(√(80)))\\\\=119,155\pm5,517.5`

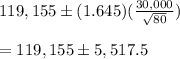
Then, the confidence interval is (119,155 + 5,517.5 , 119,155 - 5,517.5 )

= (113,637.5 , 124,672.5)

b) For a 95% confidence interval you have:

α = 1 - 0.95 = 0.05

Z_0.05/2 = Z_0.025 = 1.96

`119,155\pm (1.96)((30,000)/(√(80)))\\\\=119,155\pm 6,574.0`

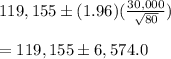
The confidence interval is (112,581 , 125,729)

c) For a 99% confidence interval:

α = 1 - 0.99 = 0.01

Z_0.01/2 = Z_0.005 = 2.58

`119,155\pm (2.58)((30,000)/(√(80)))\\\\=119,155\pm 8,653.6`

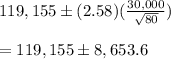
The confidence interval is (110,501.4 , 127,808.6)

d) When the confidence level increases the width of the confidence increases too. This can be noticed in the normal distribution, when the confidence level is higher, the area of the tails is reduced, and so, the confidence interval is higher.