1 Answer

Cream · Answer 1 · 2021-03-01T16:17:59+0000

Answer:

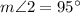
$m\angle 2=95^(\circ)$

Explanation:

It is given that ∠1 and ∠2 are a linear pair. So, there sum is 180 degrees.

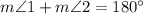$m\angle 1+m\angle 2=180^(\circ)$ ...(1)

∠2 and ∠3 are vertical angles. So, both are equal.

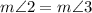$m\angle 2=m\angle 3$ ...(2)

From (1) and (2), we get

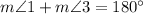
$m\angle 1+m\angle 3=180^(\circ)$

Substitute
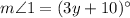$m\angle 1=(3y+10)^(\circ)$ and
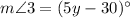$m\angle 3=(5y-30)^(\circ)$ in the above equation.

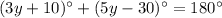
$(3y+10)^(\circ)+(5y-30)^(\circ)=180^(\circ)$

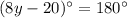
$(8y-20)^(\circ)=180^(\circ)$

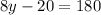
8y-20=180

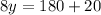
8y=180+20

Divide both sides by 8.

y=(200)/(8)

y=25

The value of y is 25.

Using equation (2), we get

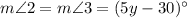
$m\angle 2=m\angle 3=(5y-30)^(\circ)$

Substitute y=25.

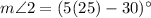
$m\angle 2=(5(25)-30)^(\circ)$

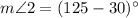
$m\angle 2=(125-30)^(\circ)$

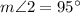
$m\angle 2=95^(\circ)$

Therefore,
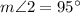$m\angle 2=95^(\circ)$ .

Please log in or register to add a comment.