Question

A student at a four-year college claims that average enrollment at four-year colleges is higher than at two-year colleges in the United States. Two surveys are conducted. Of the 35 two-year colleges surveyed, the average enrollment was 5069 with a standard deviation of 4773. Of the 35 four-year colleges surveyed, the average enrollment was 5216 with a standard deviation of 8141. Conduct a hypothesis test at the 5% level. NOTE: If you are using a Student's t-distribution for the problem, including for paired data, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, though.)Required:a. State the distribution to use for the test.b. What is the test statistic?c. What is the p-value?

Answer 1

(a) The test statistics that would be used here Two-sample t-test statistics distribution.

(b) The value of t-test statistic is 0.092.

(c) P-value of the test statistics is more than 40%.

Explanation:

We are given that of the 35 two-year colleges surveyed, the average enrollment was 5069 with a standard deviation of 4773.

Of the 35 four-year colleges surveyed, the average enrollment was 5216 with a standard deviation of 8141.

Let
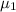`\mu_1` = average enrollment at four-year colleges in the United States.

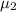`\mu_2` = average enrollment at two-year colleges in the United States.

So, Null Hypothesis,
`H_0` :
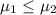`\mu_1 \leq \mu_2` {means that the average enrollment at four-year colleges is higher than at two-year colleges in the United States}

Alternate Hypothesis,
`H_A` :
`\mu_1 > \mu_2` {means that the average enrollment at four-year colleges is higher than at two-year colleges in the United States}

(a) The test statistics that would be used here Two-sample t-test statistics distribution because we don't know about population standard deviation;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p * \sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n_1_+_n_2_-_2`

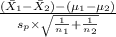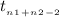
where,
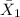`\bar X_1` = average enrollment at four-year colleges = 5216

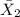`\bar X_2` = average enrollment at two-year colleges = 5069

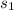`s_1` = sample standard deviation at four-year colleges = 8141

`s_2` = sample standard deviation at two-year colleges = 4773

`n_1` = sample of four-year colleges surveyed = 35

`n_2` = sample of two-year colleges surveyed = 35

Also,
`s_p= \sqrt{((n_1-1)* s_1^(2)+(n_2-1)* s_2^(2) )/(n_1+n_2-2) }` =
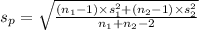`\sqrt{((35-1)* 8141^(2)+(35-1)* 4773^(2) )/(35+35-2) }` = 6672.98

So, the test statistics =
`\frac{(5216-5069)-(0)}{6672.98 * \sqrt{(1)/(35)+(1)/(35) } }` ~
`t_6_8`

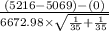= 0.092

(b) The value of t-test statistic is 0.092.

(c) P-value of the test statistics is given by the following formula;

P-value = P(
`t_6_8` > 0.092) = More than 40% as this value is not reflected in the t-table.