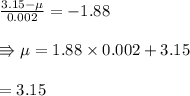Question

In a grinding operation, there is an upper specification of 3.150 in. on a dimension of a certain part after grinding. Suppose that the standard deviation of this normally distributed dimension for parts of this type ground to any particular mean dimension LaTeX: \mu\:is\:\sigma=.002 μ i s σ = .002 in. Suppose further that you desire to have no more than 3% of the parts fail to meet specifications. What is the maximum (minimum machining cost) LaTeX: \mu μ that can be used if this 3% requirement is to be met?

Answer 1

Explanation:

Let X denote the dimension of the part after grinding

X has normal distribution with standard deviation
`\sigma=0.002 in`

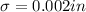
Let the mean of X be denoted by
`\mu`

there is an upper specification of 3.150 in. on a dimension of a certain part after grinding.

We desire to have no more than 3% of the parts fail to meet specifications.

We have to find the maximum
`\mu` such that can be used if this 3% requirement is to be meet

`\Rightarrow P((X- \mu)/(\sigma) <(3.15- \mu)/(\sigma) )\leq 0.03\\\\ \Rightarrow P(Z <(3.15- \mu)/(\sigma) )\leq 0.03\\\\ \Rightarrow P(Z <(3.15- \mu)/(0.002) )\leq 0.03`

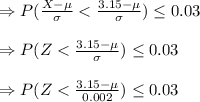
We know from the Standard normal tables that

`P(Z\leq -1.87)=0.0307\\\\P(Z\leq -1.88)=0.0300\\\\P(Z\leq -1.89)=0.0293`

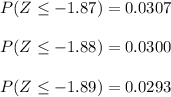
So, the value of Z consistent with the required condition is approximately -1.88

Thus we have

`(3.15- \mu)/(0.002) =-1.88\\\\\Rrightarrow \mu =1.88*0.002+3.15\\\\=3.15`