Question

A friend of mine is giving a dinner party. His current wine supply includes 11 bottles of zinfandel, 10 of merlot, and 9 of cabernet (he only drinks red wine), all from different wineries.(a) If he wants to serve 3 bottles of zinfandel and serving order is important, how many ways are there to do this?(b) If 6 bottles of wine are to be randomly selected from the 30 for serving, how many ways are there to do this?(c) If 6 bottles are randomly selected, how many ways are there to obtain two bottles of each variety?(d) If 6 bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? (Round your answer to three decimal places.)(e) If 6 bottles are randomly selected, what is the probability that all of them are the same variety? (Round your answer to three decimal places.)

Answer 1

Explanation:

(a)

Since serving order is important, we are using permutations.

Use the permutation rule with n=11

and k = 3

Number of ways to serve 3 bottles of zinfandel,

`11P_3=(11!)/((11-3)!) \\\\=(11*10*9*8!)/(8!)\\\\=11*10*9\\\\=990`

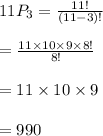
Total number of ways to serve 3 bottles of zinfandel and serving order is important is 990

(b)

Let the total number of bottles serving be, n=30

Let the number of wine bottles selected be, k = 6

Since order of serving is not in consideration for this part, use a combination.

`30C_6=(30!)/(6!* (30-6)!)\\\\=(30!)/(6!*24!) \\\\=593,775`

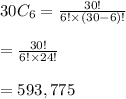
If 6 bottles of wine are to be randomly selected from the 30 for serving, total ways is 593,775

(c)

Suppose 6 bottles are randomly selected, that is, 2 from 8 bottles, 2 from 10 bottles, 2 from 12 bottles

Select 2 from 11 bottles of zinfandel in
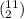`(^(11)_2)` ways

Select 2 from 10 of merlot in
`(^(10)_2)` ways

Select 2 from 9 of cabernet in
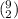`(^(9)_2)` ways

By the multiplication rule, number of ways such that two bottles of each variety is,

Number of ways is

`(^(11)_2)*(^(10)_2)*(^(9)_2)=55*45*36\\\\=89,100`

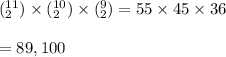
If 6 bottles are randomly selected, number of ways such that two bottles of each variety is 89,100.

(d)

Use the fraction of combinations satisfying the criterion:

Probability (selecting 2 from each variety)

`=((^(11)_2)*(^(10)_2)*(^(9)_2))/((^(30)_6)) \\\\=(55*45*36)/(593775)\\\\=0.150057\\\\\approx0.150`

If 6 bottles are randomly selected, then probability that two bottles of each variety being chosen is 0.150.

(e)

All of the of same variety means favourable outcomes

Using additional rule, the number of ways selecting 6 bottles such that all of them are of the same time from the 30 bottles

(includes 11 bottles of zinfandel, 10 of merlot, and 9 of cabernet) is

`={(^(11)_6)+(^(10)_6)+(^(9)_6)}`

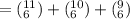
Number of ways selecting 6 bottles among 30 is
`(^(30)_6)`

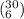
Then, the required probability is,

P(all of them are same variety)

`=\frac{{(^(11)_6)+(^(10)_6)+(^(9)_6)}}{(^(30)_6)} \\\\=(462+210+84)/(593775)\\\\=0.001273\\\\\approx0.001`

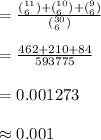
Probability that all of them are the same variety is 0.001.