Question

A news poll conducted in October 2009 surveyed a random sample of 995 adults in the United States. Of these people, 706 said they would support federal legislation putting limits on the amounts that top executives are paid at companies that receive emergency government loans. One highly paid executive claims that the percentage of U.S. adults who support limits on the amounts that executives are paid is greater than 68%. Use the P-value method with the TI-84 calculator.

Answer 1

`z=\frac{0.710 -0.68}{\sqrt{(0.68(1-0.68))/(995)}}=2.029`

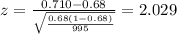
The p value would be given by:

`p_v =P(z>2.029)=0.021`

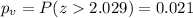
In the ti84 we follow these steps:

STAT, TESTS, 1Pro-Test

And we put the following input:

po= 0.68

x= 706, n=995 and prop
`>p_o`

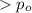
And then click on Calculate

If the significance level is higher than the p value we can reject the null hypothesis otherwise no.

Explanation:

Information given

n=995 represent the random sample taken

X=706 represent the number of people who support federal legislation putting limits on the amounts that top executives are paid at companies that receive emergency government loans

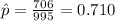`\hat p=(706)/(995)=0.710` estimated proportion of interest

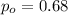`p_o=0.68` is the value that we want to test

z would represent the statistic

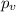`p_v` represent the p value

Hypothesis to test

We want to test if the true proportion is higher than 0.68.:

Null hypothesis:
`p\leq 0.68`

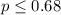
Alternative hypothesis:
`p > 0.68`

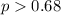
The statistic is given by:

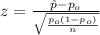`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.710 -0.68}{\sqrt{(0.68(1-0.68))/(995)}}=2.029`

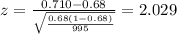
The p value would be given by:

`p_v =P(z>2.029)=0.021`

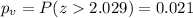
In the ti84 we follow these steps:

STAT, TESTS, 1Pro-Test

And we put the following input:

po= 0.68

x= 706, n=995 and prop
`>p_o`

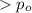
And then click on Calculate

If the significance level is higher than the p value we can reject the null hypothesis otherwise no.