Question

A county environmental agency suspects that the fish in a particular polluted lake have elevated mercury levels. To confirm that suspicion, five striped bass in that lake were caught and their tissues tested for the presence of mercury. For the purposes of comparison, four striped bass in an unpolluted lake were also caught and tested. The fish tissue mercury levels in mg/kg are given below. (Note: You may wish to use Excel for this problem.) Sample 1 (polluted lake) Sample 2 (unpolluted lake) 0.580 0.382 0.711 0.276 0.571 0.570 0.666 0.366 0.598a. Construct the 95% confidence interval for the difference in the population means based on these data.b. Test, at the 5% significance level, whether the data provide sufficient evidence to conclude that fish in the polluted lake have elevated levels of mercury in their tissue.c. Do your answers to (a) and (b) agree or disagree? Explain.

Answer 1

a. The 95% confidence interval for the difference between means is (0.071, 0.389).

b. There is enough evidence to support the claim that the fish in this particular polluted lake have signficantly elevated mercury levels.

c. They agree. Both conclude that the levels of mercury are significnatly higher compared to a unpolluted lake.

In the case of the confidence interval, we reach this conclusion because the lower bound is greater than 0. This indicates that, with more than 95% confidence, we can tell that the difference in mercury levels is positive.

In the case of the hypothesis test, we conclude that because the P-value indicates there is a little chance we get that samples if there is no significant difference between the mercury levels. This indicates that the values of mercury in the polluted lake are significantly higher than the unpolluted lake.

Explanation:

The table with the data is:

Sample 1 Sample 2

0.580 0.382

0.711 0.276

0.571 0.570

0.666 0.366

0.598

The mean and standard deviation for sample 1 are:

`M=(1)/(5)\sum_(i=1)^(5)(0.58+0.711+0.571+0.666+0.598)\\\\\\ M=(3.126)/(5)=0.63`

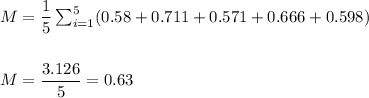
`s=\sqrt{(1)/((n-1))\sum_(i=1)^(5)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(4)\cdot [(0.58-(0.63))^2+...+(0.598-(0.63))^2]}\\\\\\ s=\sqrt{(1)/(4)\cdot [(0.002)+(0.007)+(0.003)+(0.002)+(0.001)]}\\\\\\ s=\sqrt{(0.015)/(4)}=√(0.0037)\\\\\\s=0.061`

The mean and standard deviation for sample 2 are:

`M=(1)/(4)\sum_(i=1)^(4)(0.382+0.276+0.57+0.366)\\\\\\ M=(1.594)/(4)=0.4`

`s=\sqrt{(1)/((n-1))\sum_(i=1)^(4)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(3)\cdot [(0.382-(0.4))^2+(0.276-(0.4))^2+(0.57-(0.4))^2+(0.366-(0.4))^2]}\\\\\\ s=\sqrt{(1)/(3)\cdot [(0)+(0.015)+(0.029)+(0.001)]}\\\\\\ s=\sqrt{(0.046)/(3)}=√(0.015)\\\\\\s=0.123`

Confidence interval

We have to calculate a 95% confidence interval for the difference between means.

The sample 1, of size n1=5 has a mean of 0.63 and a standard deviation of 0.061.

The sample 2, of size n2=4 has a mean of 0.4 and a standard deviation of 0.123.

The difference between sample means is Md=0.23.

`M_d=M_1-M_2=0.63-0.4=0.23`

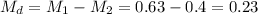
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(0.061^2)/(5)+(0.123^2)/(4)}\\\\\\s_(M_d)=√(0.001+0.004)=√(0.005)=0.07`

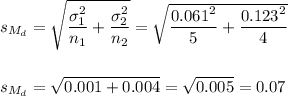
The critical t-value for a 95% confidence interval is t=2.365.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_(M_d)=2.365 \cdot 0.07=0.159`

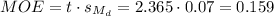
Then, the lower and upper bounds of the confidence interval are:

`LL=M_d-t \cdot s_(M_d) = 0.23-0.159=0.071\\\\UL=M_d+t \cdot s_(M_d) = 0.23+0.159=0.389`

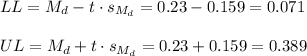
The 95% confidence interval for the difference between means is (0.071, 0.389).

Hypothesis test

This is a hypothesis test for the difference between populations means.

The claim is that the fish in this particular polluted lake have signficantly elevated mercury levels.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2> 0`

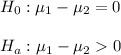
The significance level is 0.05.

The sample 1, of size n1=5 has a mean of 0.63 and a standard deviation of 0.061.

The sample 2, of size n2=4 has a mean of 0.4 and a standard deviation of 0.123.

The difference between sample means is Md=0.23.

`M_d=M_1-M_2=0.63-0.4=0.23`

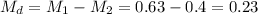
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(0.061^2)/(5)+(0.123^2)/(4)}\\\\\\s_(M_d)=√(0.001+0.004)=√(0.005)=0.07`

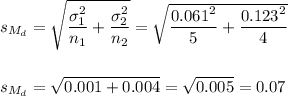
Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(0.23-0)/(0.07)=(0.23)/(0.07)=3.42`

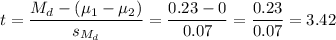
The degrees of freedom for this test are:

`df=n_1+n_2-1=5+4-2=7`

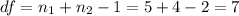
This test is a right-tailed test, with 7 degrees of freedom and t=3.42, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=P(t>3.42)=0.006`

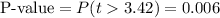
As the P-value (0.006) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the fish in this particular polluted lake have signficantly elevated mercury levels.

c. They agree. Both conclude that the levels of mercury are significnatly higher compared to a unpolluted lake.

In the case of the confidence interval, we reach this conclusion because the lower bound is greater than 0. This indicates that, with more than 95% confidence, we can tell that the difference in mercury levels is positive.

In the case of the hypothesis test, we conclude that because the P-value indicates there is a little chance we get that samples if there is no significant difference between the mercury levels. This indicates that the values of mercury in the polluted lake are significantly higher than the unpolluted lake.