Question

In the diagram, ABCD is a part of a right angled triangle ODC. If /AB/= 6 cm,

/CD/= 15cm, BC/= 8 cm, ZBCD = 90° and AB//DC, calculate, correct to 1 decimal
place, the:
2 points
1. height of triangle ODC;
Your answer
2 points
2. perimeter of triangle ODC.​

Answer 1

1) 13.3 cm

2) 48.3 cm

Explanation:

1) Right angled triangle ODC and right angled triangle OAB are similar because AB//DC. The two triangles have the same proportion and are equiangular (having equal angles) but have different lengths.

Let OB = x, OC = OB + BC = x + 8

Therefore:

`(OC)/(OB)=(DC)/(AB) \\(x+8)/(x)=(15)/(6)\\15x=6(x+8)\\15x=6x+48\\15x-6x=48\\9x=48\\x=5.3\ cm`

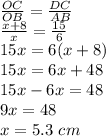
The height of triangle ODC = OC = x + 8 = 5.3 + 8 = 13.3 cm

2) Using Pythagoras theorem:

OD² = OC² + DC²

OD² = 13.3² + 15²

OD² = 401.89

OD = √401.89 = 20 cm

2) perimeter of triangle ODC = OD + OC + DC = 20 + 13.3 + 15 =48.3 cm