Question

Prove that the triangle EDF is isosceles. Give reasons for your answer.

Answer 1

The proof is shown below

Explanation:

An isosceles triangle is a triangle that have both two equal sides and two equal angles.

From the diagram to prove that triangle EDF is isosceles, we need to show that two of the angles in triangle EDF are the same.

`\angle EFD+(90+(y)/(2)) = 180(sum \ of \ angles \ in \ a \ straight \ line) \\\angle EFD=180-(90+(y)/(2))\\\angle EFD=180-90-(y)/(2)\\\angle EFD=90-(y)/(2)\\`

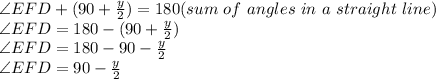
The sum of angles in a triangle is 180°. Therefore the sum of angles in triangle EDF = 180°.

`y+(90-(y)/(2) )+\angle FED = 180\\y+90-(y)/(2) +\angle FED = 180\\90+(y)/(2)+ \angle FED = 180\\\angle FED = 180-(90+(y)/(2))\\\angle FED = 180-90-(y)/(2)\\\angle FED=90-(y)/(2)`

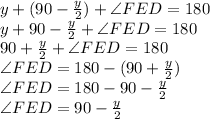
Since ∠FED and ∠EFD are equal, triangle EDF is isosceles.