Answer:
The image of the circle is 9·x² + 9·y² - 42·x + 33·y = 22
Explanation:
We convert the equation to the form (x - h)² + (y - k)² = r²
Where:
(h, k) = Coordinates of the center of the circle
We therefore have;
x² + y² - 2·x + 3·y = 8 which gives;
x² - 2·x + 1 - 1 + y² + 3·y + (3/2)² - (3/2)² = 8
(x - 1)² + (y + 3/2)² - 1 - (3/2)² = 8
(x - 1)² + (y + 3/2)² = 8 + 1 + (3/2)² = 45/4
Therefore, the center = (1, -3/2) and the radius = √5 × 3/2
The line joining the centers of the actual (1, -3/2) and reflected circle (h, k) is bisected by the line of reflection, therefore the midpoint of the line is on the line of reflection with coordinates;
Midpoint between (1, -3/2) and (h, k) =
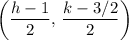
Which gives;
y = 2·x - 3 being equivalent to
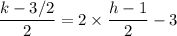
Which gives;
4·h -2·k -13 = 0.......(1)
Similarly the slope of the reflecting line is perpendicular to the line joining the centers of the actual and reflected circles
Therefore;
The slope of the line, y = 2·x - 3 = 2, hence we have;

Which gives;
2·h -4·k -12 = 0.......(2)
Multiplying equation (2) and subtracting from equation (1) gives
4·h -2·k -13 - 2×(2·h -4·k -12) = 0
6·k + 11 = 0
k = -11/6
From which we have;
2·h -4×(-11/6) -12 = 0
Hence;
h = 7/3
Therefore, the center of the reflected circle = (7/3, -11/6)
The equation of the reflected circle is therefore;
(x - 7/3)² + (y + 11/6)² = 45/4
Which gives;
9·x² + 9·y² - 42·x + 33·y - 22 = 0
or x² + y² - 42/9·x + 33/9·y = 22/9.