Answer:
Correct option: First one -> real and distinct.
Explanation:
To evaluate the roots of the equation 7x^2 + x - 1 = 0, lets find the discriminant Delta using the Bhaskara's formula:
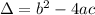
Where a, b and c are coefficients of the quadratic equation (in this case, a = 7, b = 1 and c = -1)
So we have that:

To evaluate the roots of the equation, we have the following cases:
 : Two roots real and distinct
: Two roots real and distinct
 : Two roots real and equal
: Two roots real and equal
 : Two roots not real
: Two roots not real
In our case, we have
 , so the roots are real and distinct.
, so the roots are real and distinct.
Correct option: First one