Question

How many roots does (x+10)^9 have. Please explain how u did it.

Answer 1

9

Explanation:

(x+10)^9 is the 9-degree polynomial so it has 9 roots

if it is equal to zero then it has 9 equal roots of x= -10

Answer 2

This expression contains a one root (x= -10) of multiplicity 9

Explanation:

Notice that this polynomial is given in factor form, since it is equivalent to 9 products of the same factor (x+10):

`(x+10)^9=(x+10)\,(x+10)\,(x+10)\,(x+10)\,(x+10)\,(x+10)\,(x+10)\,(x+10)\,(x+10)`

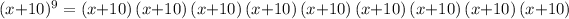
Therefore, there is a single root x = -10, since when x=-10 each of these binomial factors result in a zero.

In mathematical terms, such type of root is said to have multiplicity. And in this case, the multiplicity is "9" (the number of equal binomial factors of the polynomial form).