Answer:
Problem 2) : the gradient is "-2", and the y-intercept is "3"
Problem 3)
A is
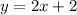
B is
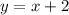
Explanation:
Problem 2)
In the line given by the equation:
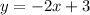
the "gradient" (also known as "slope") is the numerical coefficient that multiplies the variable "x". So in this case the gradient is "-2"
the y-intercept is the numerical term "+3" because that is the y-value result of evaluating the expression for x = 0
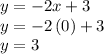
Problem 3)
Consider the two lines :
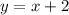and
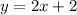
notice that both have the same y-intercept (that is the numerical term "2" at the end of both expressions. That means that both lines cross the y-axis at the point y=2.
Now notice that the gradient of one of them is "1" (for
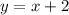) that is the coefficient that multiplies the variable "x". While for the other line (
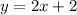) the gradient is "2" and therefore steeper than the previous one.
Then, the line identified as "A" which is the one with steeper gradient, corresponds to the equation
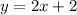, and the line identified with "B" is the one with smaller gradient
.
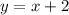