Answer:
Camera 2nd has to cover the maximum angle, i.e.
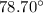 .
.
Explanation:
Please have a look at the triangular park represented as a triangle
 with sides
with sides
a = 110 ft
b = 158 ft
c = 137 ft
1st camera is located at point C, 2nd camera at point B and 3rd camera at point A respectively.
We can use law of cosines here, to find out the angles
As per Law of cosine:
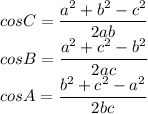
Putting the values of a,b and c to find out angles
 .
.
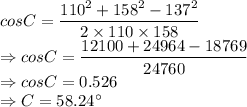


Camera 2nd has to cover the maximum angle, i.e.
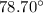 .
.