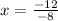Answer:
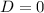
The graph has 1 x-intercept
Explanation:
Given
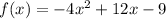
Required
- Discriminant of f
- Number of x intercepts
Let D represent the discriminant;
D is calculated as thus
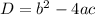
Where a, b and c are derived from the following general format;
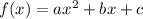
By comparing
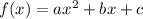 with
with
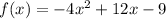
We have

Solving further;
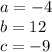
So, D can now be calculated;
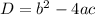 becomes
becomes
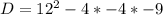
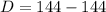
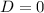
Hence, the discriminant of f is 0
From the value of the discriminant, we can determine the number of x intercepts of the graph;
When D = 0, then; there exists only one x-intercept and it as calculated as thus
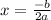
Recall that
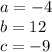
So,
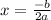 becomes
becomes