Question

. Desde el borde de una azotea de un edificio, se lanza un cuerpo hacia abajo con una velocidad de 20 m/s, si el edificio mide 105 m. ¿Cuántos segundos dura la caída?

Answer 1

t = 3.01 s

Step-by-step explanation:

In order to calculate how long it takes to the object to fall to the ground, you use the following formula, for the calculation of the height:

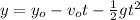`y=y_o-v_ot-(1)/(2)gt^2` (1)

yo: height of the building = 105 m

vo: initial velocity of the body = 20m/s

g: gravitational acceleration = 9.8m/s^2

t: time = ?

To find the time t, you take into account that when the body arrives to the ground the height is zero, that is, y = 0.

You replace the values of all parameters in the equation (1), and you obtain a quadratic polynomial for t:

`0=105-20t-(1)/(2)(9.8)t^2\\\\0=-4.9t^2-20t+105`

Next, you use the quadratic formula to get the roots of the polynomial:

`t_(1,2)=(-b\pm√(b^2-4ac))/(2a)`

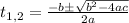
a = -4.9

b = -20

c = 105

`t_(1,2)=(-(-20)\pm√((-20)^2-4(-4.9)(105)))/(2(-4.9))\\\\t_1=3.01s\\\\t_2=-7.09s`

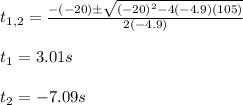
You choose the positive value t1, because it has physical meanning.

Hence, the body takes 3.01s to arrive to the ground