Answer:
a) The median AD from A to BC has a length of 6.
b) Areas of triangles ABD and ACD are the same.
Explanation:
a) A median is a line that begin in a vertix and end at a midpoint of a side opposite to vertix. As first step the location of the point is determined:
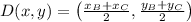
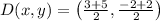
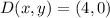
The length of the median AD is calculated by the Pythagorean Theorem:
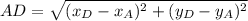
![AD = \sqrt{(4-4)^(2)+[0-(-6)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/o61pohfkahd44urg20tlap3w0nwvc9wt5e.png)
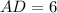
The median AD from A to BC has a length of 6.
b) In order to compare both areas, all lengths must be found with the help of Pythagorean Theorem:
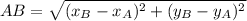
![AB = \sqrt{(3-4)^(2)+[-2-(-6)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/73m1x4o54qjl0vn6q1szatqen13arq6vth.png)
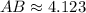
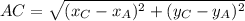
![AC = \sqrt{(5-4)^(2)+[2-(-6)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/gdf5kmbqwgul3szs7bkwdi3u1qxv63101w.png)
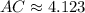
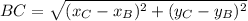
![BC = \sqrt{(5-3)^(2)+[2-(-2)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ihria5gk0xd6odar2e4yjs9gi8j11zfo1u.png)
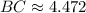
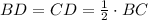 (by the definition of median)
(by the definition of median)
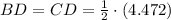
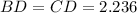
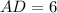
The area of any triangle can be calculated in terms of their side length. Now, equations to determine the areas of triangles ABD and ACD are described below:
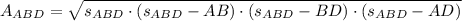 , where
, where
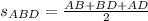
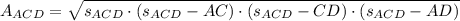 , where
, where
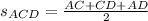
Finally,
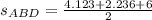
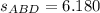
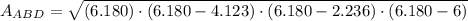
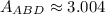
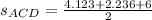
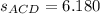
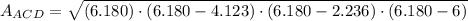
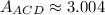
Therefore, areas of triangles ABD and ACD are the same.