Question

A student in greece discovers a pottery bowl that contains 29% of its original amount of C-14

Answer 1

The age of the pottery bowl is 12,378.7 years

Explanation:

The amount of C-14 after t yeas is given by the following equation:

`N(t) = N(0)e^(-kt)`

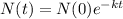
In which N(0) is the initial amount and k is the decay rate.

In this question, we have that:

`k = 0.0001`

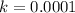
So

`N(t) = N(0)e^(-0.0001t)`

Age of the pottery bowl:

29% of its original amount of C-14. So we have to find t for which N(t) = 0.29N(0). So

`N(t) = N(0)e^(-0.0001t)`

`0.29N(0) = N(0)e^(-0.0001t)`

`e^(-0.0001t) = 0.29`

`\ln{e^(-0.0001t)} = ln(0.29)`

`-0.0001t = ln(0.29)`

`t = -(ln(0.29))/(0.0001)`

`t = 12378.7`

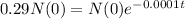
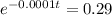
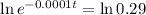
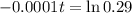
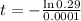
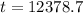
The age of the pottery bowl is 12,378.7 years