Answer:
Explanation:
Given: Circle O with BT as a tangent at point B.
T is the midpoint of arc CD.
To prove: (CA)(TB) = (TA)(CT)
Since point T is the midpoint of arc CD,
Therefore, m(arc CT) = m(arc TD)
and m∠CAT ≅ m∠DAT
m(∠ACT) = 90° [Angle subtended by the diameter]
By applying tangent rule in triangles ACT and ABT,
tan(∠CAT) =
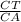
Similarly, tan(∠BAT) =

Since tan(∠CAT) = tan(∠BAT)
Therefore,
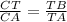
(CA) × (TB) = (CT) × (TA)
Hence proved.