Question

A boy is playing ball in a garden surrounded by a wall 2.5 m high kicks the ball vertically up from a height of 0.4 m with a spee d of 14 m/s.For how long is the ball above the height of the wall .

Answer 1

2.5 sec

Explanation:

Height of wall = 2.5 m

initial speed of ball = 14 m/s

height from which ball is kicked = 0.4 m

we calculate the speed of the ball at the height that matches the wall first

height that matches wall = 2.5 - 0.4 = 2.1 m

using
`V^(2)` =
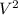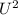`U^(2)` + 2as

where a = acceleration due to gravity = -9.81 m/s^2 (negative in upwards movement)

`V^(2)` =
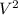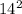`14^(2)` + 2(-9.81 x 2.1)

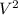`V^(2)` = 196 - 41.202

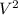`V^(2)` = 154.8

v =
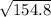`√(154.8)` = 12.44 m/s

this is the velocity of the ball at exactly the point where the wall ends.

At the maximum height, the speed of the ball becomes zero

therefore,

u = 12.44 m/s

v = 0 m/s

a = -9.81 m/s^2

t = ?

using V = U + at

0 = 12.44 - 9.81t

-12.44 = -9.81

t = -12.44/-9.81

t = 1.27 s

the maximum height the ball reaches will be gotten with

`V^(2)` =
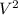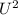`U^(2)` + 2as

a = -9.81 m/s^2

0 =
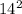`14^(2)` + 2(-9.81s)

0 = 196 - 19.62s

s = -196/-19.62 = 9.99 m. This the maximum height reached by the ball.

height from maximum height to height of ball = 9.99 - 2.5 = 7.49 m

we calculate for the time taken for the ball to travel down this height

a = 9.81 m/s^2 (positive in downwards movement)

u = 0

s = 7.49 m

using s = ut +
`(1)/(2)`a
`t^(2)`

7.49 = (0 x t) +
`(1)/(2)`(9.81 x
`t^(2)` )

7.49 = 0 + 4.9
`t^(2)`

`t^(2)` = 7.49/4.9 = 1.53

t =
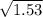`√(1.53)` = 1.23 sec

Total time spent above wall = 1.27 s + 1.23 s = 2.5 sec