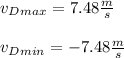Question

A transverse, wave travelling on a chord is represented by D=0.22sin (5.6x+34t) where D and x are inmeters and t is in seconds. For this wave, determine; a) wavelength b) frequency c) velocity (both magnitude and direction) d) amplitude e) maximum and minimum speed of particles in the chord.

Answer 1

a) λ = 1.12 m

b) f = 5.41 Hz

c) v = 154.54 m/s

d) A = 0.22m

e)

`v_D_(max)=7.48(m)/(s)\\\\v_D_(min)=-7.48(m)/(s)\\\\`

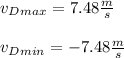
Step-by-step explanation:

You have the following equation for a wave traveling on a cord:

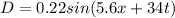`D=0.22sin(5.6x+34t)` (1)

The general expression for a wave is given by:

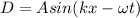`D=Asin(kx-\omega t)` (2)

By comparing the equation (1) and (2) you have:

A: amplitude of the wave = 0.22m

k: wave number = 5.6 m^-1

w: angular velocity = 34 rad/s

a) The wavelength is given by substitution in the following expression:

`\lambda=(2\pi)/(k)=(2\pi)/(5.6m^(-1))=1.12m`

b) The frequency is:

`f=(\omega)/(2\pi)=(34s^(-1))/(2\pi)=5.41Hz`

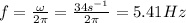
c) The velocity of the wave is:

`v=(\omega)/(k)=(34s^(-1))/(0.22m^(-1))=154.54(m)/(s)`

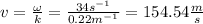
d) The amplitude is 0.22m

e) To calculate the maximum and minimum speed of the particles you obtain the derivative of the equation of the wave, in time:

`v_D=(dD)/(dt)=(0.22)(34)cos(5.6x+34t)\\\\v_D=7.48cos(5.6x+34t)`

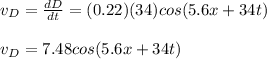
cos function has a minimum value -1 and maximum +1. Then, you obtain for maximum and minimum velocity:

`v_D_(max)=7.48(m)/(s)\\\\v_D_(min)=-7.48(m)/(s)\\\\`