Answer:
[see below]
For "slope-point" form:
Slope point (also called "Point-slope") form is:

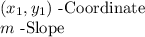
Finding the Slope:
We need to find the slope of the line given.
Slope is:
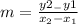
We are given the points (2,-1) and (-2,-2).
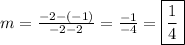
The slope of the line is 1/4.
Creating the Point-Slope Equation:
Replace 'm' with 1/4 and '(x1, y1)' with (2, -1).
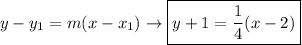
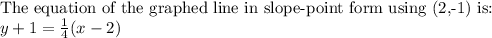
Creating the Slope Intercept Form Equation:
Slope intercept form is:

We can convert our point slope equation into slope intercept form.

The equation of the line in slope intercept form is:
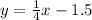 OR
OR
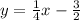 .
.