Answer:
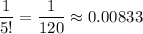 .
.
Explanation:
Note that all five letters here are distinct (i.e., none of them is repeated.) There are
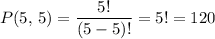 ways to arrange five distinct items (where the order of the arrangement matters.)
ways to arrange five distinct items (where the order of the arrangement matters.)
The reason is that there are five choices for the first item, four choices for the second item, three choices for the third item, etc. Hence, the numerator is
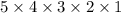 , which is the same as
, which is the same as
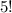 . On the other hand, since there's only one way to choose five items out of five (i.e., to select them all,) the denominator would be
. On the other hand, since there's only one way to choose five items out of five (i.e., to select them all,) the denominator would be
 .
.
Note that the
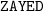 is just one of that
is just one of that
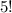 possible permutations. If the cards are arranged in random, all these permutations ought to have an equal probability. Therefore:
possible permutations. If the cards are arranged in random, all these permutations ought to have an equal probability. Therefore:
 .
.