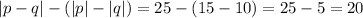Question

Given that p=9i+12j and q=-6i-8j. Evaluate |p-q|-q

Answer 1

`|p-q|-(|p|-|q|) = 20`

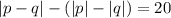
Explanation:

First let's find the value of 'p-q':

`p - q = 9i + 12j - (-6i - 8j)\\p - q = 9i + 12j + 6i + 8j\\p - q = 15i + 20j\\`

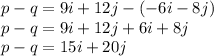
To find |p-q| (module of 'p-q'), we can use the formula:

`|ai + bj| = \sqrt{a^(2)+b^(2)}`

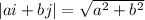
Where 'a' is the coefficient of 'i' and 'b' is the coefficient of 'j'

So we have:

`|p - q| = |15i + 20j| = \sqrt{15^(2)+20^(2)} = 25`

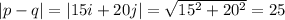
Now, we need to find the module of p and the module of q:
`|p| = |9i + 12j| = \sqrt{9^(2)+12^(2)} = 15`

`|q| = |-6i - 8j| = \sqrt{(-6)^(2)+(-8)^(2)} = 10`

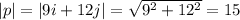
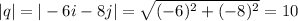
Then, evaluating |p-q|-, we have:

`|p-q|-(|p|-|q|) = 25 - (15 - 10) = 25 - 5 = 20`